VanderPolPlots.m

Contents

Overview

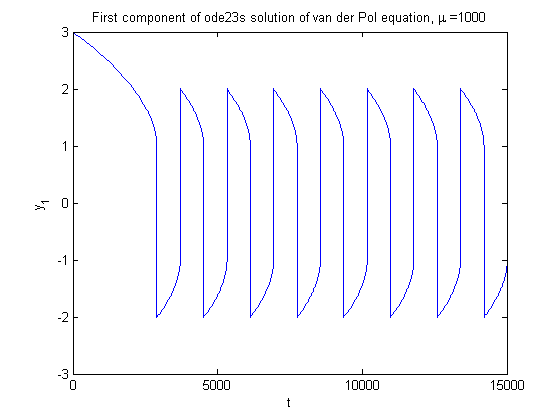
Provides plots of the solution of the Van der Pol equation

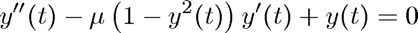
$$ y''(t) - \mu\left(1-y^2(t)\right)y'(t) + y(t) = 0 $$

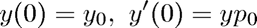
$$ y(0) = y_0,\ y'(0) = yp_0 $$

for various values of 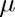$\mu$.

The stiff solver ode23s is used for all solutions.

Beginning of code

Initialize

clear all
close all
f = @(t,y,mu) [y(2); mu*(1 - y(1)^2)*y(2) - y(1)];
t0 = 0;
y0 = [3 0];    % initial condition
tol = 1e-4;
opts = odeset('RelTol',tol);
%for mu=[0 0.1 0.2 1 10 20]
for mu=[1000]
    tmax = 5*max(20, 3*mu);
    [t,y] = ode23s(f,[t0 tmax],y0,opts,mu);
    figure, plot(t,y(:,1))
    title(strcat('First component of ode23s solution of van der Pol equation, \mu = ',num2str(mu)));
    xlabel('t');
    ylabel('y_1');
    pause
    figure, plot(y(:,1),y(:,2))
    %axis equal
    title(strcat('Phase plot of ode23s solution of van der Pol equation, \mu = ',num2str(mu)));
    xlabel('y_1');
    ylabel('y_2');
    pause
end


© Greg Fasshauer, IIT. Published with MATLAB® 7.12