VanderPolDemo.m
Contents
Overview
This script illustrates the stiffness of the Van der Pol equation
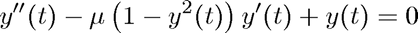
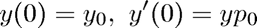
Beginning of code
Initialize
clear all close all f = @(t,y,mu) [y(2); mu*(1 - y(1)^2)*y(2) - y(1)]; t0 = 0; y0 = [2 0]; % initial condition tol = 1e-4;
Example 1
We use 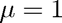 , which results in a non-stiff problem which ode23 can easily handle
, which results in a non-stiff problem which ode23 can easily handle
tmax = 20; mu = 0; opts = odeset('RelTol',tol); ode23(f,[t0 tmax],y0,opts,mu); title(strcat('ode23 solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y'); legend('y_1','y_2')

Plot of first component (position) vs. time
pause [t,y] = ode23(f,[t0 tmax],y0,opts,mu); plot(t,y(:,1),'-o'); title(strcat('First component of ode23s solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y_1');
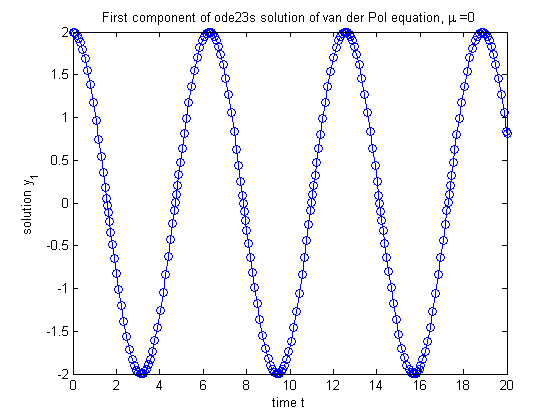
Solving the same problem with ode23s
pause ode23s(f,[t0 tmax],y0,opts,mu); title(strcat('ode23s solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y'); legend('y_1','y_2') pause
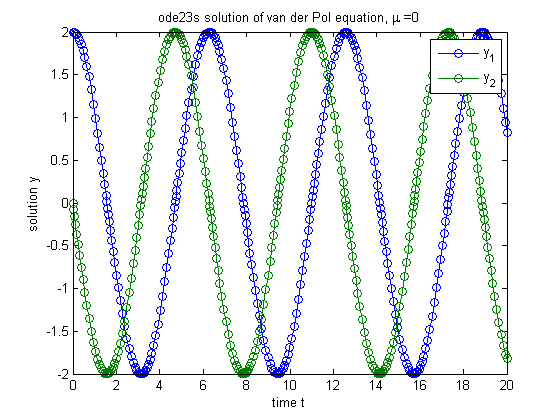
Example 2
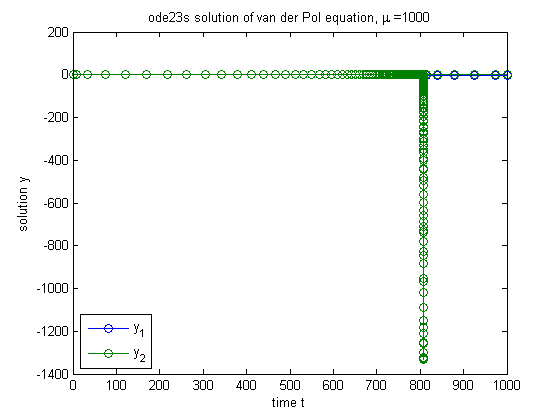
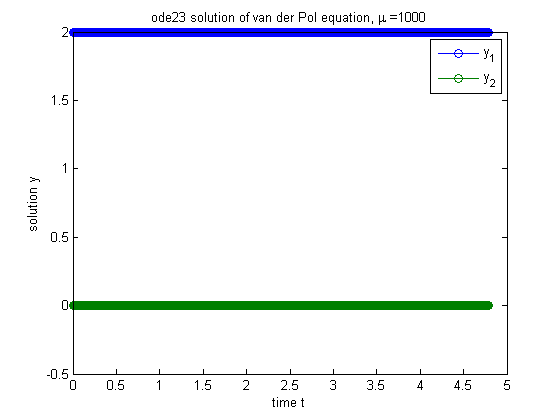
If we change 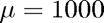 , then the problem becomes stiff, and we need see that ode23 is very slow. Note the short
, then the problem becomes stiff, and we need see that ode23 is very slow. Note the short 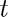 -range in the plot. The stiff solver ode23s does a much better job below.
-range in the plot. The stiff solver ode23s does a much better job below.
tmax = 1000; mu = 1000; opts = odeset('RelTol',tol); ode23(f,[t0 tmax],y0,opts,mu); title(strcat('ode23 solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y'); legend('y_1','y_2')
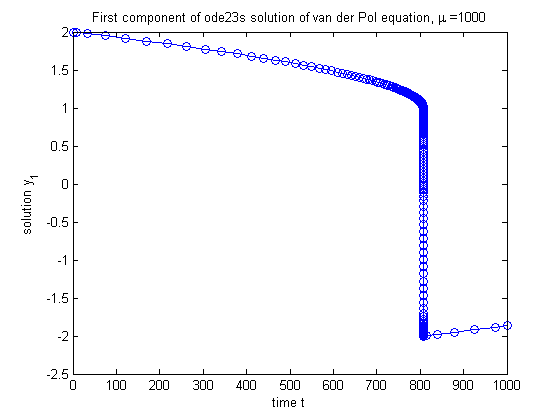
Plot of first component (position) vs. time (using ode23s)
pause [t,y] = ode23s(f,[t0 tmax],y0,opts,mu); plot(t,y(:,1),'-o'); title(strcat('First component of ode23s solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y_1');
Solving the same problem with ode23s
pause ode23s(f,[t0 tmax],y0,opts,mu); title(strcat('ode23s solution of van der Pol equation, \mu = ',int2str(mu))); xlabel('time t'); ylabel('solution y'); legend('y_1','y_2','Location','SouthWest') pause