SkydiveDemo.m
Contents
Overview
This script illustrates the solution of a first-order IVP:
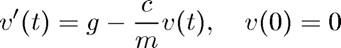
with analytical solution
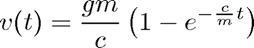
for finding the terminal velocity of a skydiver. Here 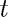 stands for time,
stands for time, 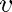 for velocity, and
for velocity, and
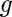 : gravitational constant
: gravitational constant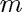 : mass
: mass : drag coefficient
: drag coefficient
The right-hand side function is coded in Skydive.m
Initialization
clear all clc close all g = 9.81; m = 68.1; c = 12.5; % specific constants v = @(t) (g*m/c) * (1 - exp(-(c/m)*t)); % analytical solution f = @Skydive; % function handle for right-hand side function t0 = 0; y0 = 0; % initial time and initial velocity tend = 15; % end time N = 100; % number of time steps h = (tend-t0)/N; % stepsize
Call Euler
We will discuss this function later
[t,y] = Euler(t0,y0,f,h,N);
Plot
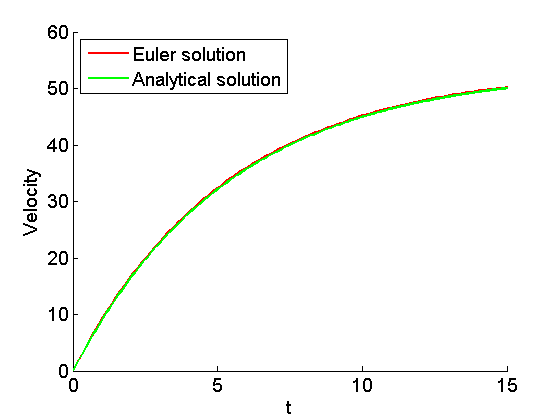
figure hold on set(gca,'Fontsize',14) xlabel('t','FontSize',14); ylabel('Velocity','FontSize',14); plot(t,y,'r','LineWidth',2); % Euler solution
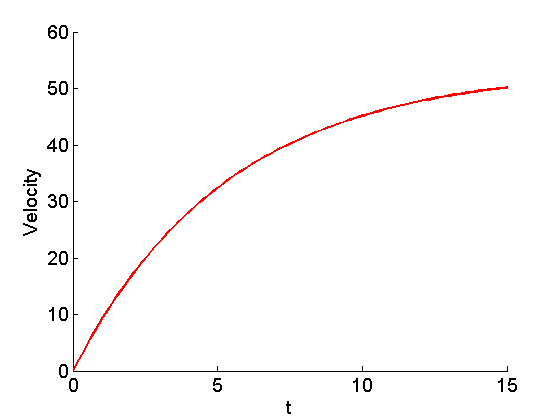
pause tt=linspace(t0,tend,201); plot(tt,v(tt),'g','LineWidth',2); % analytical solution legend('Euler solution','Analytical solution','Location','NorthWest'); hold off disp(sprintf('Terminal velocity: %f m/s.', g*m/c))
Terminal velocity: 53.444880 m/s.