Skydive3Demo.m
Contents
Overview
This script illustrates the solution of a system of first-order IVPs:
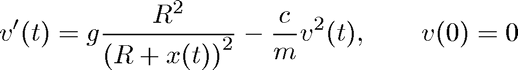

for finding the terminal velocity of a skydiver (without parachute). Here 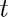 stands for time,
stands for time, 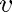 for velocity,
for velocity, 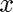 for altitude, and
for altitude, and
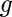 : gravitational constant
: gravitational constant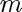 : mass
: mass : seond-order drag coefficient
: seond-order drag coefficient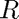 : radius of earth
: radius of earth
The right-hand side function is coded in Skydive3.m
Skydive3Event.m contains the stopping criterion (to be used via event handling) for the ODE solver ode23 used below. We stop when altitude = 0.
Beginning of code
Initialize
clear all close all t0 = 0; y0 = [4000; 0]; % initial time, position and velocity tend = 100; % end time g = 9.81; % gravitational constant (in m/s^2) c = 0.225; % drag coefficient (in kg/m) m = 68.1; % mass of skydiver (in kg) R = 6.37e6; % radius of earth
Event handling lets us determine the time when altitude = 0
opts = odeset('events',@Skydive3Event);
Solve ODE system coded in Skydive3.m
See how we now use all arguments for ode23:
- the right-hand side (vector) function Skydive3
- the time interval [t0 tend]
- the initital condition (vector) y0
- the event handling option set using odeset
- other parameters for Skydive3, i.e., g, c, m, and R
[t,y,te,ye] = ode23(@Skydive3,[t0 tend],y0,opts,g,c,m,R);
Note how the time for the event (altitude = 0) is returned in te and the altitude and velocity are returned in the vector ye, i.e., the impact velicity is given by ye(2).
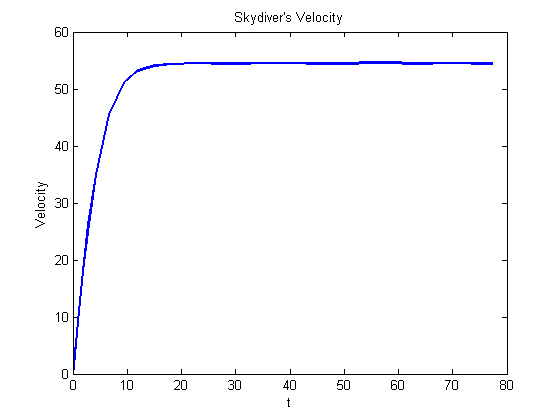
disp(sprintf('The skydiver hits the ground after %4.2f seconds with a velocity of %4.2f m/s.',... te,ye(2)))
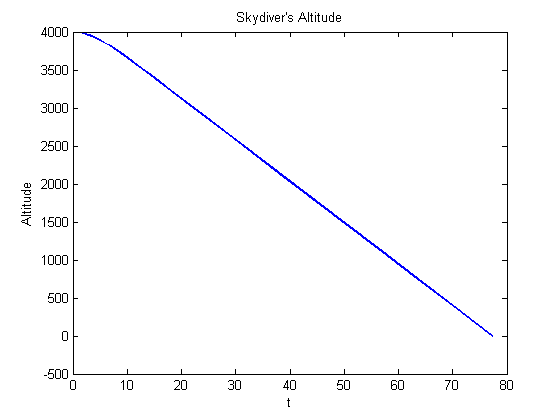
The skydiver hits the ground after 77.29 seconds with a velocity of 54.44 m/s.
Plot velocity, y(:,2), of skydiver
figure plot(t,y(:,2),'LineWidth',2); title('Skydiver''s Velocity') xlabel('t') ylabel('Velocity') pause
Plot altitude, y(:,1), of skydiver
figure plot(t,y(:,1),'LineWidth',2); title('Skydiver''s Altitude') xlabel('t') ylabel('Altitude')