SecantDemo.m

Contents

Overview

Illustrates the secant method coded in secant.m to solve 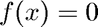$f(x)=0$ near the two initial guesses 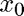$x_0$ and $x_1$.

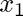Find a root of the Bessel function 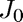$J_0$

We use the built-in MATLAB function besselj to solve

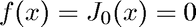
$$ f(x) = J_0(x) = 0 $$

Note that the secant method requires two initial guesses. Here we use

$$ x_0 = 0.1, \quad x_1 = 0.5 $$

Note how secant.m needs functions as input arguments.

disp('Find a root of the Bessel function J0:')
J0 = @(x) besselj(0,x);
disp('Initial guesses are x0 = 0.1, x1 = 0.5')
[x,iter] = secant(J0,[0.1 0.5]);
disp(sprintf('A root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))
x = [0:.1:30];
plot(x, besselj(0,x))

Find a root of the Bessel function J0:
Initial guesses are x0 = 0.1, x1 = 0.5
x2 = 6.85908459790363
x3 = 9.79493381399967
x4 = 8.50658069581209
x5 = 8.69675460128128
x6 = 8.65398507702502
x7 = 8.65372719408842
x8 = 8.65372791292170
x9 = 8.65372791291101
x10 = 8.65372791291101
A root of J0 is x = 8.653728.
It was computed in 10 iterations.

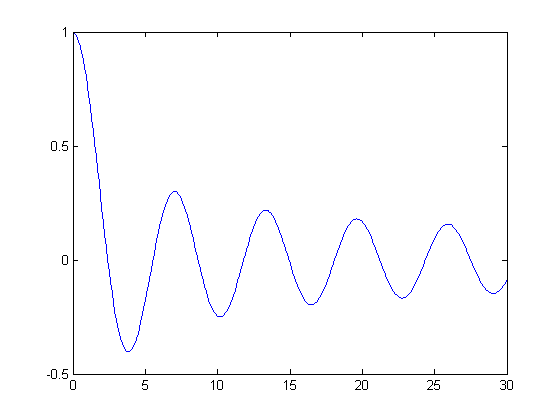
Find the first positive root of the Bessel function 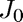$J_0$

Notice how the previous example did not produce the first positive root. In order to get that, we need to change our initial guess. We now use

$$ x_0 = 1.0, \quad x_1 = 4.0 $$

The rest is the same as above (and therefore not even repeated in the code).

%pause
disp('Find the first positive root of the Bessel function J0:')
disp('Initial guesses are x0 = 1, x1 = 4')
[x,iter] = secant(J0,[1 4]);
disp(sprintf('The first positive root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))

Find the first positive root of the Bessel function J0:
Initial guesses are x0 = 1, x1 = 4
x2 = 2.97496279446610
x3 = 1.20601365422573
x4 = 2.49126712130979
x5 = 2.41179960026729
x6 = 2.40469143790313
x7 = 2.40482575314659
x8 = 2.40482555770122
x9 = 2.40482555769577
x10 = 2.40482555769577
The first positive root of J0 is x = 2.404826.
It was computed in 10 iterations.

Compute 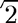$\sqrt{2}$

We solve the equation

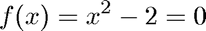
$$ f(x) = x^2 - 2 = 0 $$

where we use the two initial guesses

$$ x_0 = 1, \quad x_1 = 2 $$

%pause
disp('Compute sqrt(2):')
sqr2 = @(x) x^2-2;
disp('Initial guesses are x0 = 1, x1 = 2')
[x,iter] = secant(sqr2,[1 2]);
disp(sprintf('sqrt(2) = %f was computed in %d iterations.\n',x,iter))

Compute sqrt(2):
Initial guesses are x0 = 1, x1 = 2
x2 = 1.33333333333333
x3 = 1.40000000000000
x4 = 1.41463414634146
x5 = 1.41421143847487
x6 = 1.41421356205732
x7 = 1.41421356237310
x8 = 1.41421356237310
sqrt(2) = 1.414214 was computed in 8 iterations.


© Greg Fasshauer, IIT. Published with MATLAB® 7.11