RK4Demo.m

Overview
Code

Overview

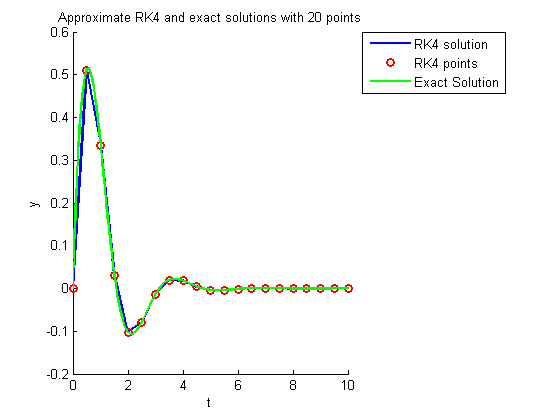
This script illustrates the use of the classical fourth-order Runge-Kutta method (implemented in the function RK4.m) for the problem

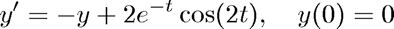
$y' = -y + 2 e^{-t}\cos(2t),\quad y(0)=0$

on the interval $[0,10]$ with exact solution

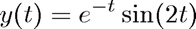
$y(t) = e^{-t}\sin(2t)$

Code

Set up the problem

clear all
close all
f = @(t,y) -y+2*exp(-t).*cos(2*t);
t0=0; y0=0;    % initial condition
tmax = 10;
Nvalues = [20 100 500];

Run for several different values of 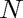$N$ , the number of steps used to reach the final time $t=10$ .

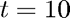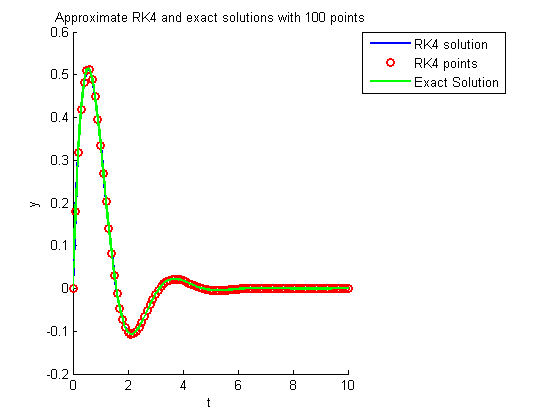
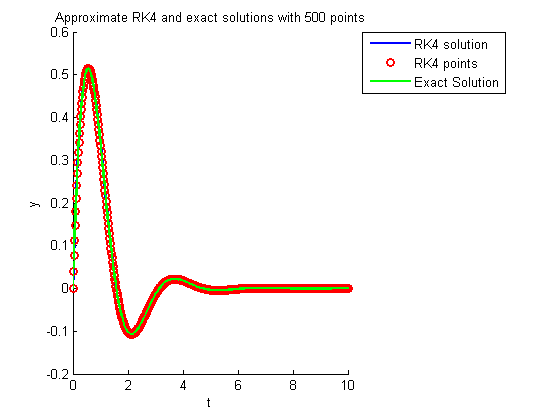
for N=Nvalues
    h=tmax/N;
    [t,y] = RK4(t0,y0,f,h,N);   % call RK4.m
    figure
    hold on
    title(sprintf('Approximate RK4 solution with %d points',N))
    xlabel('t'), ylabel('y')
    xlim([t0 tmax]), ylim([-0.2 0.6])
    plot(t,y,'b','LineWidth',2);
    plot(t,y,'ro','LineWidth',2);
    legend('RK4 solution','RK4 points',-1);
    pause
    title(sprintf('Approximate RK4 and exact solutions with %d points',N))
    tt=linspace(0,10,201);
    plot(tt,exp(-tt).*sin(2*tt),'g','LineWidth',2);  % exact solution
    legend('RK4 solution','RK4 points', 'Exact Solution',-1);
    hold off
    if N<Nvalues(end)
        pause
    end
end

RK4Demo.m

Contents

Overview

Code