PolyfitDemo.m
Contents
Overview
Illustrates the use of the MATLAB built-in function polyfit to perform a polynomial least squares fit to data coming from the quadratic polynomial
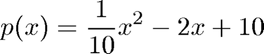
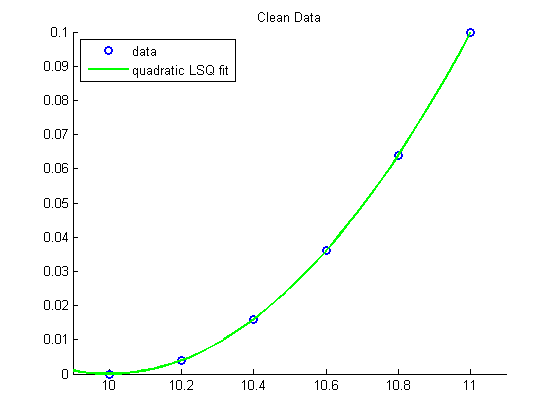
Example 1: Fit "clean" data using a quadratic polynomial
We should expect an exact answer
clear all close all x = [10:0.2:11]'; y = [0:0.2:1]'.^2/10; disp('Clean Data') hold on plot(x, y, 'bo', 'LineWidth',2) xlim([9.9 11.1]) ylim([0 0.1]) u = linspace(9.9,11.1,50); % Fit with a degree 2 polynomial disp('Fitting with quadratic polynomial') p = polyfit(x,y,2) disp(sprintf('p(x) = %3.2fx^2 + %3.2fx + %3.2f',p)) % evaluate the resulting polynomial v = polyval(p,u); plot(u, v, 'g-', 'LineWidth', 2) legend('data','quadratic LSQ fit','Location','NorthWest') title('Clean Data') hold off
Clean Data
Fitting with quadratic polynomial
p =
0.1000 -2.0000 10.0000
p(x) = 0.10x^2 + -2.00x + 10.00
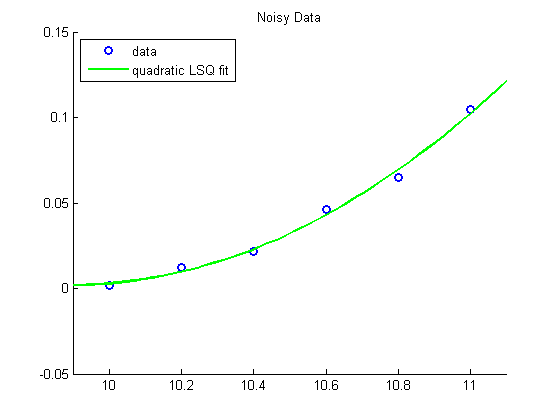
Example 2: Fit "noisy" data using a quadratic polynomial
%pause disp('Noisy Data') % Add 10% noise to the data y = y + 0.1*max(y)*rand(size(y)); figure hold on plot(x, y, 'bo', 'LineWidth',2) xlim([9.9 11.1]) ylim([-0.05 0.15]) u = linspace(9.9,11.1,50); % Fit with a degree 2 polynomial disp('Fitting with quadratic polynomial') p = polyfit(x,y,2); disp(sprintf('p(x) = %3.2fx^2 + %3.2fx + %3.2f',p)) % evaluate the resulting polynomial v = polyval(p,u); plot(u, v, 'g-', 'LineWidth', 2) legend('data','quadratic LSQ fit','Location','NorthWest') title('Noisy Data') %pause
Noisy Data Fitting with quadratic polynomial p(x) = 0.08x^2 + -1.62x + 8.01
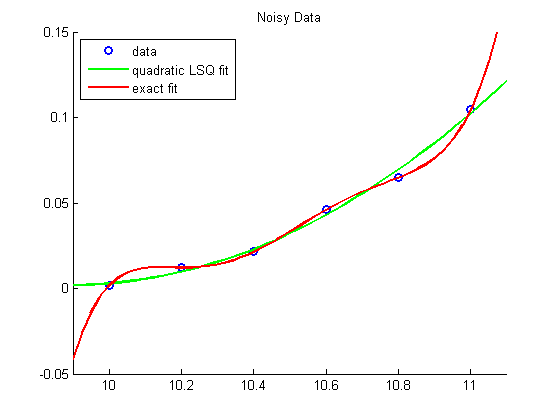
Example 3: Fit "noisy" data using a degree 5 polynomial
disp('Fitting with quintic polynomial') p = polyfit(x,y,5); disp(sprintf('p(x) = %3.2fx^5 + %3.2fx^4 + %3.2fx^3 + %3.2fx^2 + %3.2fx + %3.2f',p)) % evaluate the resulting polynomial v = polyval(p,u); plot(u, v, 'r-', 'LineWidth', 2) legend('data','quadratic LSQ fit','exact fit','Location','NorthWest') hold off
Fitting with quintic polynomial
Warning: Polynomial is badly conditioned. Add points with distinct X
values, reduce the degree of the polynomial, or try centering
and scaling as described in HELP POLYFIT.
p(x) = 2.24x^5 + -117.54x^4 + 2465.11x^3 + -25842.33x^2 + 135417.99x + -283765.89