NewtonDemo.m
Contents
Overview
Illustrates Newton's method coded in newton.m to solve 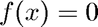 near the initial guess
near the initial guess 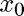 .
.
Find a root of the Bessel function 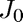
We use the built-in MATLAB function besselj to solve
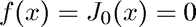
Note that Newton's method also requires the derivative
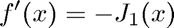
and an initial guess. Here we use
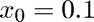
Note how newton.m needs functions as input arguments.
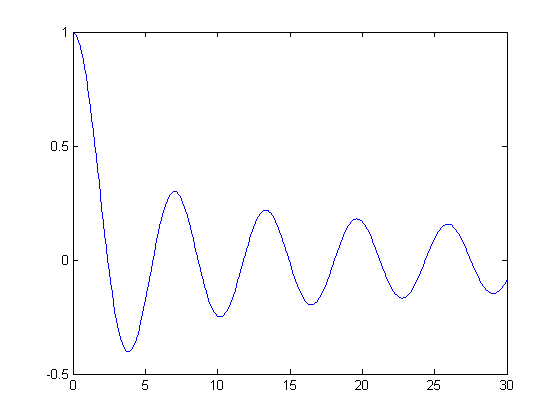
disp('Find a root of the Bessel function J0:') J0 = @(x) besselj(0,x); J0prime = @(x) -besselj(1,x); disp('Initial guess is x0 = 0.1') [x,iter] = newton(J0,J0prime,0.1); disp(sprintf('A root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter)) x = [0:.1:30]; plot(x, besselj(0,x))
Find a root of the Bessel function J0: Initial guess is x0 = 0.1 x1 = 20.07498957681857 x2 = 22.12298141969568 x3 = 20.79398411189246 x4 = 21.23307459842233 x5 = 21.21162251204526 x6 = 21.21163662987456 x7 = 21.21163662987926 x8 = 21.21163662987926 A root of J0 is x = 21.211637. It was computed in 8 iterations.
Find the first positive root of the Bessel function 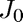
Notice how the previous example did not produce the first positive root. In order to get that, we need to change our initial guess. We now use
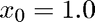
The rest is the same as above (and therefore not even repeated in the code).
%pause disp('Find the first positive root of the Bessel function J0:') disp('Initial guess is x0 = 1.0') [x,iter] = newton(J0,J0prime,1); disp(sprintf('The first positive root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter)) %pause
Find the first positive root of the Bessel function J0: Initial guess is x0 = 1.0 x1 = 2.73888573574470 x2 = 2.36778795983232 x3 = 2.40455555120498 x4 = 2.40482554254401 x5 = 2.40482555769577 x6 = 2.40482555769577 The first positive root of J0 is x = 2.404826. It was computed in 6 iterations.
Compute 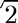
We solve the equation
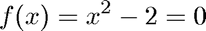
where we again need the derivative
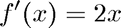
We use three different initial guesses:
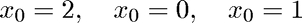
disp('Compute sqrt(2):') sqr2 = @(x) x^2-2; sqr2prime = @(x) 2*x; disp('Initial guess is x0 = 2.0') [x,iter] = newton(sqr2,sqr2prime,2); disp(sprintf('sqrt(2) = %f was computed in %d iterations.\n',x,iter)) %pause disp('Initial guess is x0 = 0') [x,iter] = newton(sqr2,sqr2prime,0); %pause disp('Initial guess is x0 = 1.0') [x,iter] = newton(sqr2,sqr2prime,1); disp(sprintf('sqrt(2) = %f was computed in %d iterations.\n',x,iter))
Compute sqrt(2): Initial guess is x0 = 2.0 x1 = 1.50000000000000 x2 = 1.41666666666667 x3 = 1.41421568627451 x4 = 1.41421356237469 x5 = 1.41421356237310 x6 = 1.41421356237309 sqrt(2) = 1.414214 was computed in 6 iterations. Initial guess is x0 = 0 Newton iteration failed since derivative is zero. Initial guess is x0 = 1.0 x1 = 1.50000000000000 x2 = 1.41666666666667 x3 = 1.41421568627451 x4 = 1.41421356237469 x5 = 1.41421356237310 x6 = 1.41421356237309 sqrt(2) = 1.414214 was computed in 6 iterations.