MatchDemo.m
Contents
Overview
This script illustrates the solution of the burning match problem
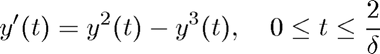
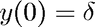
along with the fact that this becomes a stiff problem when the initial radius of the flame, 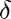 , becomes very small.
, becomes very small.
Beginning of code
Initialize
clear all close all f = @(t,y) y^2-y^3; t0 = 0; tol = 1e-4; opts = odeset('RelTol',tol);
Example 1
Use ode23tx to solve the problem with
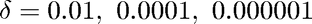
and note how ode23tx takes forever toadvance the solution for 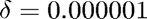
dvalues = [0.01 0.0001 0.000001]; for delta=dvalues tmax=2/delta; y0=delta; % initial condition ode23tx(f,[t0 tmax],y0,opts); title(sprintf('ode23tx with delta=%f',delta)) pause end
Example 2
Now use the stiff solver ode23s to solve the same problem.
for delta=dvalues tmax=2/delta; y0=delta; % initial condition ode23s(f,[t0 tmax],y0,opts); title(sprintf('ode23s with delta=%f',delta)) pause end
