FzeroDemo.m

Contents

Overview

Illustrates the NCM routine fzerotx (textbook version of fzero) to solve 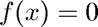$f(x)=0$ on the interval $[x_0, x_1]$.

Find a root of the Bessel function 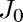$J_0$

We use the built-in MATLAB function besselj to solve

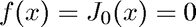
$$ f(x) = J_0(x) = 0 $$

Note that the routine fzero (Brent's method) requires an initial interval. Here we use

$$ [x_0,x_1] = [0,3] $$

Note how fzerotx.m needs functions as input arguments.

disp('Find the first positive root of the Bessel function J0:')
J0 = @(x) besselj(0,x);
disp('Initial interval is [a,b] = [0,3]')
x = fzerotx(J0,[0,3]);
disp(sprintf('The first positive root of J0 is x = %f.\n',x))

Find the first positive root of the Bessel function J0:
Initial interval is [a,b] = [0,3]
The first positive root of J0 is x = 2.404826.

Compute 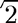$\sqrt{2}$

We solve the equation

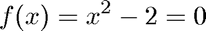
$$ f(x) = x^2 - 2 = 0 $$

where we use the initial interval

$$ [x_0,x_1] = [0,2] $$

pause
disp('Compute sqrt(2):')
sqr2 = @(x) x^2-2;
disp('Initial interval is [a,b] = [0,2]')
x = fzerotx(sqr2,[0,2]);
disp(sprintf('sqrt(2) = %f.',x))

Compute sqrt(2):
Initial interval is [a,b] = [0,2]
sqrt(2) = 1.414214.


Published with MATLAB® 7.9