FminDemo.m
Contents
Overview
Illustrates the NCM routine fmintx (textbook version of fminbnd) to find a local minimum of 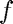 on the interval
on the interval ![$[x_0, x_1]$](FminDemo_eq78075.png) .
.
First Example: Find a local minimum of the Bessel function 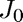
We use the interval ![$[x_0,x_1] = [0,30]$](FminDemo_eq05420.png)
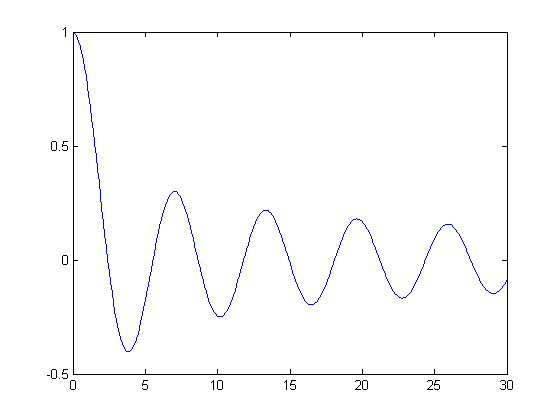
disp('Find a local minimum of the Bessel function J0:') J0 = @(x) besselj(0,x); disp('Interval is [a,b] = [0,30]') fmintx(J0,0,30); x = fmintx(J0,0,30); disp(sprintf('A local minimum of J0 is %f attained at x = %f.\n',J0(x),x)) x = [0:.1:30]; plot(x, besselj(0,x))
Find a local minimum of the Bessel function J0: Interval is [a,b] = [0,30] A local minimum of J0 is -0.249705 attained at x = 10.173468.
Second Example: Find the absolute minimum of the Bessel function 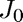
The previous example demonstrated that fzerotx (or fminbnd) may not be able to find the global minimum. We use therefore need to use a tighter interval. We pick ![$[x_0,x_1] = [0,10]$](FminDemo_eq58206.png) .
.
%pause disp('To find the absolute minimum of the Bessel function J0') J0 = @(x) besselj(0,x); disp('we need to adjust the interval to [a,b] = [0,10]') x = fmintx(J0,0,10); disp(sprintf('The minimum of J0 is %f attained at x = %f.\n',J0(x),x))
To find the absolute minimum of the Bessel function J0 we need to adjust the interval to [a,b] = [0,10] The minimum of J0 is -0.402759 attained at x = 3.831706.
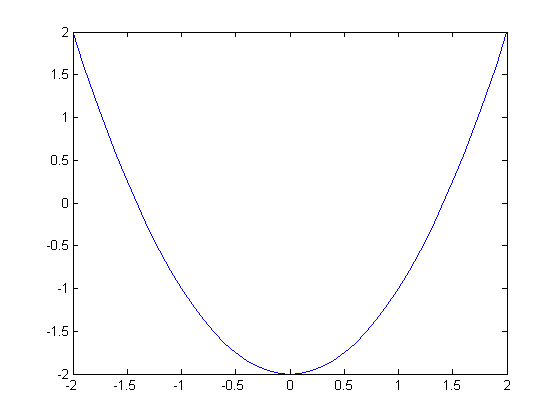
Second Example: Find the minimum of the function 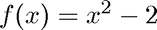
We use the interval ![$[x_0,x_1] = [-2,2]$](FminDemo_eq10986.png)
%pause disp('Compute the minimum of f(x)=x^2-2:') sqr2 = @(x) x.^2-2; disp('Interval is [a,b] = [-2,2]') x = fmintx(sqr2,-2,2); disp(sprintf('Minimum of f is %f attained at x=%f.',sqr2(x),x)) x = [-2:.1:2]; plot(x, sqr2(x))
Compute the minimum of f(x)=x^2-2: Interval is [a,b] = [-2,2] Minimum of f is -2.000000 attained at x=-0.000000.